PINN反演NS方程
2024/7/23
整个代码实现基于 Pytorch 。
问题定义 #
Navier-Stokes 方程定义如下: $$ u_t+\lambda_1(uu_x+vu_y)=-p_x+\lambda_2(u_{xx}+u_{yy}), $$
$$ v_t+\lambda_1(uv_x+vv_y)=-p_y+\lambda_2(v_{xx}+v_{yy}). $$
式中,$u(t,x,y)$是$x$轴的速度场,$v(t,x,y)$是$y$轴的速度场,$p(t,x,y)$是压力场,三者都是非定常的。参数$\lambda=(\lambda_1,\lambda_2)$是需要反演的未知参数,真实值分别为 $1$ 和 $0.01$。
网络的输出应该为三维$(u,v,p)$,但由于 Navier-Stokes 的解满足下面散度为 0 的方程,即: $$ u_x+v_y=0. $$ 速度场$u$和$v$又可以看做流量场的导数,即: $$ u=\psi_y,v=-\psi_x. $$ 因此,网络的输出维度可以由三维转变为二维$(\psi,p)$。
网络模型定义 #
采用 MLP 来实现 PINN 的神经网络模型,隐藏层的激活函数选择 Tanh。
class PINN(nn.Module):
def __init__(self, input_size, hidden_size, output_size, depth=8, act=nn.Tanh):
super(PINN, self).__init__()
layers = [torch.nn.Linear(input_size, hidden_size), act()]
for i in range(depth):
layers.append(torch.nn.Linear(hidden_size, hidden_size))
layers.append(act())
layers.append(torch.nn.Linear(hidden_size, output_size))
self.layers = nn.Sequential(*layers)
def forward(self, x):
return self.layers(x)读取解析解 #
对于逆问题,即方程中的某些参数未知。若只知道 PDE 方程及边界条件,PDE 参数未知,该逆问题为非定问题,所以必须要知道其他信息,如部分观测点的解。
这里的解析解数据来源于 PINN 原作者 Maziar Raissi 的 GitHub:maziarraissi/PINNs: Physics Informed Deep Learning。
由于本实现没有去做验证,所以这里没有读取 p 的标签数据。
def initData():
N_train = 5000
# 获取训练数据集
data = scipy.io.loadmat('./data/cylinder_nektar_wake.mat')
U_label = data['U_star'].astype(np.float32) # N x 2 x T
# p_label = data['p_star'].astype(np.float32).flatten()[:, None] # N x T
t_label = data['t'].astype(np.float32).flatten()[:, None] # T x 1
X_label = data['X_star'].astype(np.float32) # N x 2
N = X_label.shape[0]
T = t_label.shape[0]
x = np.tile(X_label[:, 0:1], (1, T)).flatten()[:, None] # NT x 1
y = np.tile(X_label[:, 1:2], (1, T)).flatten()[:, None] # NT x 1
t = np.tile(t_label, (1, N)).T.flatten()[:, None] # NT x 1
u = U_label[:, 0, :].flatten()[:, None] # NT x 1
v = U_label[:, 1, :].flatten()[:, None] # NT x 1
idx = np.random.choice(N * T, N_train, replace=False)
x_train = torch.from_numpy(x[idx, :]).requires_grad_(True)
y_train = torch.from_numpy(y[idx, :]).requires_grad_(True)
t_train = torch.from_numpy(t[idx, :]).requires_grad_(True)
X_train = torch.cat([x_train, y_train, t_train], dim=1)
u_train = torch.from_numpy(u[idx, :]).flatten().requires_grad_(True)
v_train = torch.from_numpy(v[idx, :]).flatten().requires_grad_(True)
X_train = X_train.to(device)
u_train = u_train.to(device)
v_train = v_train.to(device)
return X_train, u_train, v_train损失函数 #
PDE 方程的偏差项可定义为: $$ f:=u_t+\lambda_1(uu_x+vu_y)=-p_x+\lambda_2(u_{xx}+u_{yy}), $$
$$ g:=u_t+\lambda_1(uu_x+vu_y)=-p_x+\lambda_2(u_{xx}+u_{yy}). $$
损失主要包括偏微分结构损失(PDE loss)和真实数据条件损失(Data loss): $$ PDE\ loss:=\frac{1}{N}\sum^N_{i=1}(\mid u(t^i,x^i,y^i)-u^i\mid^2+\mid v(t^i,x^i,y^i)-v^i\mid^2), $$
$$ Data\ loss:=\frac{1}{N}\sum^N_{i=1}(\mid f(t^i,x^i,y^i)\mid^2+\mid g(t^i,x^i,y^i)\mid^2), $$
$$ MSE:=PDE\ loss+Data\ loss. $$
def NS_PDE_1(u, v, du_dx, du_dy, du_dt, du_dxx, du_dyy, dp_dx, l1, l2):
return du_dt + l1 * (u * du_dx + v * du_dy), -dp_dx + l2 * (du_dxx + du_dyy)
def NS_PDE_2(u, v, dv_dx, dv_dy, dv_dt, dv_dxx, dv_dyy, dp_dy, l1, l2):
return dv_dt + l1 * (u * dv_dx + v * dv_dy), -dp_dy + l2 * (dv_dxx + dv_dyy)
def d(f, x):
return torch.autograd.grad(f, x,
grad_outputs=torch.ones_like(f),
retain_graph=True,
create_graph=True)[0]
def loss_func():
global index # 计数
optimizer_adam.zero_grad()
optimizer_lbfgs.zero_grad()
# 第一部分loss:内点非物理产生的loss PDE loss
psi_and_p = model(X_train)
psi = psi_and_p[:, 0:1]
p = psi_and_p[:, 1:2]
# 求psi对x、y的导数得到u、v
U = d(psi, X_train)
u = U[:, 1]
v = -U[:, 0]
# 使用自动求导方法得到u、v对x、y、t的导数
du_dX = d(u, X_train)
dv_dX = d(v, X_train)
du_dx = du_dX[:, 0]
du_dy = du_dX[:, 1]
du_dt = du_dX[:, 2]
dv_dx = dv_dX[:, 0]
dv_dy = dv_dX[:, 1]
dv_dt = dv_dX[:, 2]
# 使用自动求导方法得到p对x、y的导数
dp_dX = d(p, X_train)
dp_dx = dp_dX[:, 0]
dp_dy = dp_dX[:, 1]
# 使用自动求导方法得到u、v对x、y的二阶导数
du_dXX = d(du_dX, X_train)
du_dxx = du_dXX[:, 0]
du_dyy = du_dXX[:, 1]
dv_dXX = d(dv_dX, X_train)
dv_dxx = dv_dXX[:, 0]
dv_dyy = dv_dXX[:, 1]
left_1, right_1 = NS_PDE_1(u, v, du_dx, du_dy, du_dt, du_dxx, du_dyy, dp_dx, lambda_1, lambda_2)
left_2, right_2 = NS_PDE_2(u, v, dv_dx, dv_dy, dv_dt, dv_dxx, dv_dyy, dp_dy, lambda_1, lambda_2)
loss_PDE_1 = criterion(left_1, right_1)
loss_PDE_2 = criterion(left_2, right_2)
loss_PDE = loss_PDE_1 + loss_PDE_2
# 第二部分loss:Data loss
loss_data_u = criterion(u, u_train)
loss_data_v = criterion(v, v_train)
loss_data = loss_data_u + loss_data_v
loss = loss_PDE + loss_data
loss.backward()
if index % 100 == 0:
print(index, lambda_1.item(), lambda_2.item(), loss.item())
index = index + 1
return loss训练 #
网络一共包含 9 个隐藏层,每层 20 个隐藏单元。优化算法采用 Adam,通过 Xavier 进行模型的权重初始化。并将方程中的未知参数添加到优化器中进行训练。
模型非常难收敛,一共进行了 20 万次 epoch 的训练。
def train(model, epochs_adam):
model.train()
for epoch in range(epochs_adam):
optimizer_adam.step(loss_func)
def init_weights(m):
if type(m) == nn.Linear:
nn.init.xavier_uniform_(m.weight)
device = torch.device("cuda") if torch.cuda.is_available() else torch.device("cpu")
input_size = 3
hidden_size = 20
output_size = 2
epochs_adam = 200000
index = 1
model = PINN(input_size, hidden_size, output_size)
model.apply(init_weights)
model.to(device)
criterion = torch.nn.MSELoss()
optimizer_adam = torch.optim.Adam(model.parameters(), lr=0.001)
X_train, u_train, v_train = initData()
# lambda_1 = 1
lambda_1 = torch.tensor(np.array([0])).float().to(device).requires_grad_(True)
lambda_1.grad = torch.ones((1)).to(device)
# lambda_2 = 0.01
lambda_2 = torch.tensor(np.array([0])).float().to(device).requires_grad_(True)
lambda_2.grad = torch.ones((1)).to(device)
# 将未知参数添加进优化器中进行训练
optimizer_adam.add_param_group({'params': lambda_1, 'lr': 0.00001})
optimizer_adam.add_param_group({'params': lambda_2, 'lr': 0.00001})
train(model, epochs_adam)结果 #
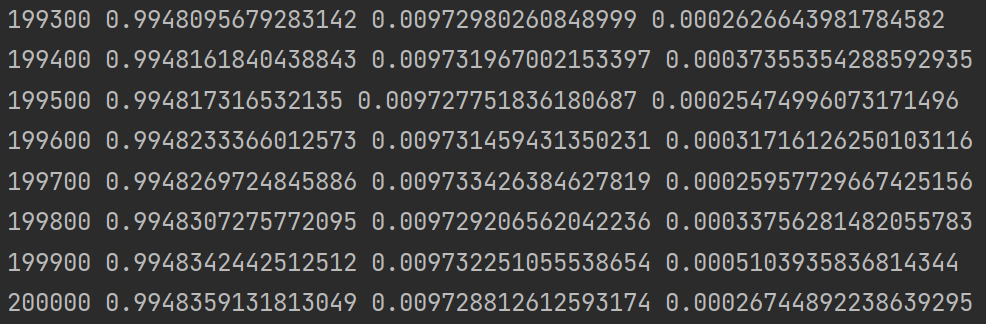
第一个打印值为当前的 epoch,第二个为$\lambda_1$,第三个为$\lambda_2$,最后一个为 loss。可以发现经过 20 万次训练,模型才能几近收敛。最终训练得到的$\lambda_1\approx0.99$,$\lambda_2\approx0.0097$,都非常接近真实解 $1$ 和 $0.01$。